The effect of bottom topography

The evolution of a certain vorticity distribution w(x,y,t) is determined by several physical effects (for those available in nsevol, see this page), and one of these is the presence of a bottom topography.

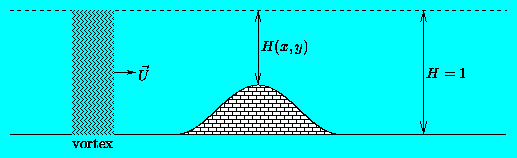
The model used by nsevol describes fluid motions in a two-dimensional (2D) plane: the method is two-dimensional. It thus seems strange that it is possible to add effects of a topography, since a topography is essentially a three-dimensional thing. Yet, it is possible since in a 2D-model topography can be represented by an "extra term" in the equations. This is of course only possible if the topography does not alter the fluid motions too much: the assumption of 2D motions must remain valid. Hence, the topography cannot be too high (for mountains) or too deep (for troughs).

An illustration

Introducing an artificial third dimension for illustrative purposes only, the "side view" of a case with a topographic ridge looks like this:

In this picture, H(x,y) represents the fluid depth, which by default is H=1 (in dimensionless units). Suppose now that a vortex approaches the ridge: what happens to it?

If the fluid is inviscid there is conservation of potential vorticity:

          w + f
         ------- = constant
            H 

  where: w(x,y) = relative vorticity distribution
         f(x,y) = Coriolis parameter (background rotation)
         H(x,y) = fluid depth

When the vortex climbs up the ridge, the fluid depth decreases and from this conservation law it then follows that the vortex becomes weaker: w decreases in absolute value (assume that f is constant for a moment). At the same time the "length" of the vortex decreases. Since the fluid is considered to be incompressible, this means that the vortex becomes wider as it climbs the ridge. And when the vortex descends the ridge again, its strength increases and it becomes narrower again.

Since the motions in the numerical model are two-dimensional, the squeezing and stretching of the vortex is absent, but the other effects -- weakening and widening as it climbs the ridge -- are certainly taking place. This is clearly visible in an example of a Lamb dipole crossing a ridge, which is without background rotation.

Background rotation

If the background rotation f is not constant, then more complex effects occur, but the basics of the above is the same. The main difference is that positive and negative vortex patches are affected in a different way. This is clearly visible in an example of a Lamb dipole crossing a ridge -- with background rotation.

See also the cases where a Bessel monopole encounters a north-south ridge or a circular mountain.

Some further remarks

In general the fluid shows viscous effects, which weaken the vortex as time goes on, hence the potential vorticity is not conserved. The above mentioned effects of weaking and widening due to a topographic mountain will nevertheless take place.
If the topography is a trough, i.e. if H>1 at some places, a vortex will of course grow stronger and become smaller as it descends into the trough, and weaken and widen as it climbs out of it again.
For the assumption of two-dimensional motions, the value of H should always be of the order 1, say 0.5<H<2, depending on the nature of the topography (e.g. on how steep it is).
The numerical method used is a finite difference method, which means that only more or less smooth topographies are possible.

<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.

Jos van Geffen -- Home | Site Map | Contact Me