Vortex Evolution with a Finite Difference Method

Vortex Evolution with a
Finite Difference Method

The evolution of a two-dimensional (2D) vorticity distribution is described by the 2D Navier-Stokes equation in the vorticity-streamfunction formulation. One of the possible methods to solve this so-called vorticity equation is a Finite Difference Method, which applies discretisation of the vorticity equation on a grid in a finite domain. Such a method is relatively easy to program and can handle a great variety of initial vorticity distributions, ranging from single vortices (e.g. monopole, dipole) to a vorticity field covering the whole domain (e.g. uniform, random). The density of the grid and the time step determine the accuracy of the computation.

The program is named nsevol; you see its logo at the top of this page. Since it uses the Navier-Stokes equation to compute the evolution of a certain vorticity distribution, the program's name is to be pronounced as 'en-es-evol'.

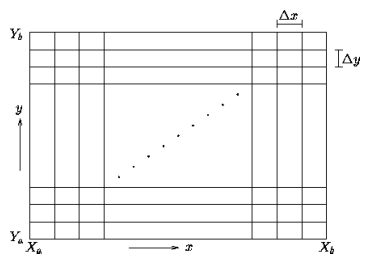
A rectangular domain is discretided in the x and y direction, respectively; the grid cells do not need to be square. The value of the vorticity is then computed on each grid point as a function of time, using a finite time step. In practice the number of grid cells in either direction is 2ⁿ. Boundary conditions apply simultaneously to opposite boundaries.

The Finite Difference Method includes non-linear and viscous effects:

Non-linear effects describe the change of vorticity due to the flow field of the vorticity itself, which either increase or decrease the velocities.
Viscosity diffuses the vorticity: it is spread over a larger area and its extrema are reduced, resulting in lower velocities.

Background rotation, an external flow and/or a bottom topography can be included as well. The method also gives the possibility to follow the motion of passive tracers, like is done in experiments with particles or blobs of dye. Positioning tracers in the program can be done in a variety of ways: in a blob, as separate particle and/or as a contour line.

The non-linear term is programmed such that energy, enstrophy and skew-symmetry are conserved for the case of zero viscosity.

The time integration scheme used (see below) makes the Finite Difference Method very stable: as long as the velocities on the grid are not too large, i.e. as long as the time step is not too big, there are no difficulties. In practice, the Courant number CFL -- a measure for the maximum velocity somewhere on the grid -- must be smaller than the square root of 3 in the case when there is no viscosity; if viscosity is present, then CFL can be somewhat larger. (In the inviscid case it is even possible to compute backwards in time using a negative time step.)

The following boundary conditions can be applied:

stress-free
fluid cannot go through the boundary, but it can move along the boundary without friction.
"membrane"
fluid can move freely through the boundary, but it cannot move along the boundary.
periodicity
fluid that leaves the domain on one side, re-enters the domain on the opposite side.
no-slip
fluid cannot go through the boundary and it cannot move along the boundary either due to friction, i.e. the velocity is equal to zero at the boundary.

Notes:

-- Boundary conditions 2 is not really relevant for the study of vortex dynamics for which the program is intended.

-- Condition 3 is (unfortunately) not available when there is a bottom topography.

There are pages available with:

- a list of

- some information on running the program 'nsevol'.

The numerical scheme

The time evolution of the vorticity equation is computed with an explicit third-order Runge-Kutta scheme, where viscous term is discretised with a Crank-Nicolson scheme and the nonlinear term with the Arakawa scheme. The streamfunction is found from the vorticity by solving the Poisson equation with a Fourier Analysis and Cyclic Reduction (FACR) routine if there is no bottom topography. If there is a bottom topography a 'modified Poisson equation' must be solved, which cannot be done by FACR. For that purpose, a NAG routine using a multigrid method is applied. (The latter routine is unfortunately a factor of about 10 slower than FACR.) In either case, the routine solving the streamfunction limits the choice in the number of grid cells to 2ⁿ in either direction.

The basis of this numerical scheme follows from a code developed by Paulo Orlandi and Roberto Verzicco (Rome, Italy). The routines solving the streamfunction are added during my work in Eindhoven and Dundee. Also added is: a great number of initial vorticity distributions, passive tracers, background rotation, bottom topography, and output of several extra characteristics of the flow. To analyse the results, several additional programs are available.

<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.

Jos van Geffen -- Home | Site Map | Contact Me