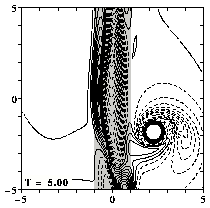

Consider the same initial situation as on Bessel monopole encounters a north-south ridge but now with f0=+3, which means that the ridge is on the northern hemisphere.
For all graphs: positive contours (0.1 to 2.0 at an interval of 0.1) are drawn solid, negative contours (-0.1 to -2.0 at an interval of -0.1) are drawn dashed, and the zero contour is dotted. Since the maximum of vorticity at the centre of the monopole is much larger than 2.0, the vortex looks like a "hole".
Note that the domain measures 20 by 20 length units -- the graphs show only the central part of this domain.
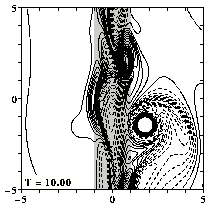
Turning on the time evolution means that the monopole moves to the north-west, due to the beta-effect, and it encounters the ridge. Due to the strong topography effect, there is now a creation of much stronger relative vorticity over the ridge and the monopole is completely torn apart (destroyed) by the ridge:
At T=25 (middle graph of the last row) you can still recognize the
vortex, but the maximum of vorticity is then no longer at the location
of that vortex but elsewhere in the domain.
At T=0 a passive tracer was placed at the centre of the monopole.
The maximum of vorticity and the tracer move along together until
about T=23: then the maximum of vorticity moves away from the tracer.
The tracer is at the ridge until the end of the run (T=50),
indicating that the remains of the vortex stay on the ridge:
Trajectory of the tracer (red) initially placed at the maximum of
vorticity and of that maximum of vorticity (blue). The latter is drawn
only until about T=27; it has left the location of the tracer at
about T=23. The position of the tracer is given until T=50.
The green line shows the monopole's trajectory in the shown part of
the domain in the absence of the topography.
This MPEG movie (0.5 Mb; 101 frames) featuring the evolution from T=0 until T=50, shows far more clearly the effect of the ridge on the monopole
The background for this enormous difference in evolution between a run with f0=0 and the above one with f0=+3 is the much larger deformation of the contours of potential vorticity by the ridge for f0=+3:
For f0=+3 the monopole is completely surrounded by positive potential vorticity and the gradient of potential vorticity at the ridge is very strong, too strong for the monopole to cross it.
For f0=-3 the gradient of potential vorticity at the ridge is also very strong, but the effect is very different.
===> Bessel monopole encounters a north-south ridge -- with f0=-3.
<=== Bessel monopole encounters a north-south ridge -- with f0=0.
Note:
If the ridge is a trough, i.e. if h_max<0, then the effect
shown above -- the rebound of the vortex by the topography -- occurs
at positive f0.
The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me