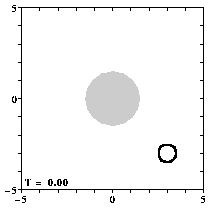
Contours of relative vorticity of the initial situation.
The location of the circular mountain is shown by the shaded region.
(You can click on the pictures for a larger version.)

A monopolar vortex, such as the Bessel monopole, will move in the presence of a background rotation, due to the Coriolis force, as explained on the page about a Bessel monopole on a beta-plane. The rotation effects are described in the model with the Coriolis parameter f=f0+beta*y. The value of f0 does not matter for that simulation since there is no bottom topography example. If there is a bottom topography, then things can be quite different.
In the simulations presented here the monopole encounters a circular mountain, as it travels to the north-west due to the beta-effect.

Contours of relative vorticity of the initial situation.
The location of the circular mountain is shown by the shaded region.
(You can click on the pictures for a larger version.)
For all graphs: positive contours (0.1 to 2.0 at an interval of 0.1) are drawn solid, negative contours (-0.1 to -2.0 at an interval of -0.1) are drawn dashed, and the zero contour is dotted. Since the maximum of vorticity at the centre of the monopole is much larger than 2.0, the vortex looks like a "hole".
Note that the domain measures 20 by 20 length units -- the graphs show only the central part of this domain.
Turning on the time evolution means that the monopole moves to the north-west, due to the beta-effect, and it encounters the mountain:
The monopole then starts climbing the mountain. First it goes to the south-west, then to the north, after which it leaves the mountain. In this process the monopole is somewhat deformed to a little elliptic, but it recorvers very well.
The monopole then leaves the mountain and continues its travel to the north-west.
This MPEG movie (0.5 Mb; 101 frames) featuring the evolution from T=0 until T=50, shows far more clearly the effect of the mountain on the monopole.
The monopole's motion across the mountain and its maximum of vorticity are shown in these graphs:
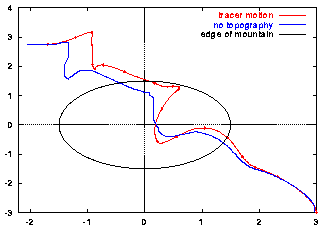
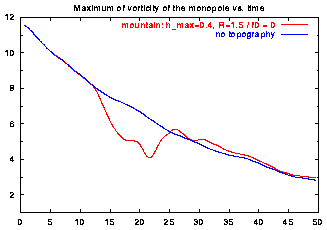
The monopole's rotation about its centre and its motion through the domain create a flow across the topography. This does not mean, however, that relative vorticity is created at the mountain -- as is the case for a uniform flow across a mountain -- since f0=0 in this case.
As a result, the mountain does not have much effect on the monopole's evolution. This is no longer true if the constant f0 in the Coriolis parameter is non-zero.
A value f0=0 means that the mountain is located at the equatior (y=0). For f0 less than zero the mountain is at the southern hemisfere and for f0 larger than zero it is at the northern hemisphere -- which makes quite a difference. The following examples show a very different flow evolution:
===> Bessel monopole encounters a circular
mountain -- with f0=-3.
===> Bessel monopole encounters a circular
mountain -- with f0=+3.
The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me