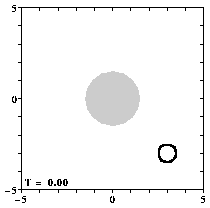
Bessel monopole encounters a circular mountain
f0=-3: southern hemisphere

The simulation discussed on the pabe Bessel monopole encounters a circular mountain is with f0=0 in the Coriolis paramter. This means that the ridge is located at the equator. For non-zero f0-values, the monopole's evolution can be quite different, depending on the f0-value.

Consider the same initial situation as on Bessel monopole encounters a circular mountain but now with f0=-3, which means that the ridge is on the southern hemisphere.

For all graphs: positive contours (0.1 to 2.0 at an interval of 0.1) are drawn solid, negative contours (-0.1 to -2.0 at an interval of -0.1) are drawn dashed, and the zero contour is dotted. Since the maximum of vorticity at the centre of the monopole is much larger than 2.0, the vortex looks like a "hole".
Note that the domain measures 20 by 20 length units -- the graphs show only the central part of this domain.

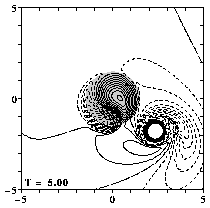
Turning on the time evolution means that the monopole moves to the north-west, due to the beta-effect.

The motion of the monopole and its rotation about its centre results in a flow across the mountain, similar to the case of a uniform flow across a mountain, and relative vorticity is generated. Since f0 is negative, the fluid moving away from the mountain gets negative relative vorticity and the fluid moving onto the mountain gets positive relative vorticity.

The monopole reaches the mountain, surrounded by a "ring" of negative vorticity (a result of the Rossby waves it leaves behind as it moves due to the beta-effect). The mountain is "covered" in positive vorticity and the monopole cannot climb the mountain very far:

The monopole is deflected to the north by the mountain. At T=20 the monopole's centre has climbed the mountain for about 1/3-rd of the mountain's radius: that is as far as it gets. The monopole descends the mountain and leaves it behind:

After this, the monopole continues its motion to the north-west.

This MPEG movie (0.5 Mb; 101 frames) featuring the evolution from T=0 until T=50, shows far more clearly the effect of the mountain on the monopole.

The monopole's motion across the mountain and its maximum of vorticity are shown in these graphs:

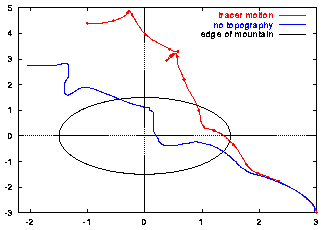
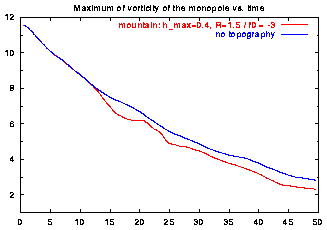
Motion of a tracer (red curve) initially placed at the maximum of vorticity of the monopole (where it remains all the time) when the monopole encounters the mountain. Dots are placed along the curve at every 2.5 time units. Note that the scales on both axes differ -- the mountain is circular! The blue line is the monopole's path due to the beta-effect only.
 
Right: Maximum of vorticity versus time of the monopole crossing the mountain (red) and in the case of no topography (blue). The maximum of vorticity reaches the foot of the mountain at about T=12.5 and it leaves the mountain shortly after T=20.

This mountain, in combination with f0=-3, evidently deflects the monopole east of the mountain.

For positive f0-values, i.e. a mountain on the northern hemisphere, things are quite different.
===> Bessel monopole encounters a circular mountain -- with f0=+3.

<=== Bessel monopole encounters a circular mountain -- with f0=0.

For details on simulations with different f0-values and heights, see:
Van Geffen, J.H.G.M. and Davies P.A.: 1999,
"A monopolar vortex encounters an isolated topographic feature on a beta-plane,"
Dynam. Atmosph. & Oceans, in press.

The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.

===> Some details on the computation presented on this page for those who are interested.

<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.

 
Jos van Geffen -- Home  |  Site Map  |  Contact Me

created: 21 April 1998
last modified: 26 May 2001