Contours of relative vorticity of the initial situation.
(You can click on the pictures for a larger version.)

A monopolar vortex, such as the Bessel monopole, does not move when there is no background rotation: it then merely rotates about its centre. In the presence of a background rotation which varies with latitude, however, the monopole moves. This is due to the Coriolis force, caused by the rotation of the system.
For the Earth, for instance, the Coriolis force varies with the latitude and this effect that affects the motion of vortices (high and low pressure areas) in the atmosphere: on the northern hemisphere low pressure areas (=cyclonic vortices) tend to move to the north-west and high pressure areas (=anti-cyclonic) tend to move to the south-west. This motion is of course partly counteracted by the overall eastward wind in the upper atmosphere, the jet stream.
This effect can clearly be seen in the following simulation.

Contours of relative vorticity of the initial situation.
(You can click on the pictures for a larger version.)
For all graphs: positive contours (0.1 to 2.0 at an interval of 0.1) are drawn solid, negative contours (-0.1 to -2.0 at an interval of -0.1) are drawn dashed, and the zero contour is dotted. Since the maximum of vorticity at the centre of the monopole is much larger than 2.0, the vortex looks like a "hole".
Note that the domain measures 20 by 20 length units -- the graphs show only the central part of this domain.
The rotation effects are described in the model with the Coriolis parameter f=f0+beta*y. The value of f0 does not matter for this simulation (there is no bottom topography). The value of beta is 0.3. And since the monopole is positive (cyclonic) it moves to the north-west:
===> MPEG movie (0.5 Mb; 101 frames) showing the evolution from T=0 until T=50.
As the monopole moves, it leaves behind vorticity in the form of so-called Rossby waves, and the monopole interacts with this vorticity again. The result is that the monopole does not move along a straight line, as this graph of its x,y-position shows:
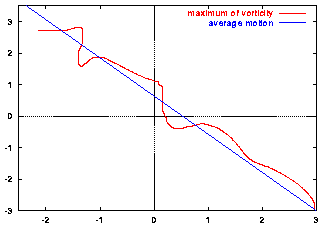
Red line: motion of the maximum of vorticity through the domain;
it starts from the bottom-right corner.
Blue line: average motion.
The larger beta is, the faster is the decay of the
vortex. The overall motion, however, is the same for all
beta.
The monopole also decays due to viscous effects. But a change of the
Reynolds number does not affect the direction of the motion, only
the distance covered in a certain time period.
===> Bessel monopole encounters a north-south
ridge
===> Bessel monopole encounters a circular
mountain
f = 2*Omega*sin(phi)
with: Omega = rotation rate
phi = latitude
In a 2D model, like used here, this is at a reference latitude
phi0:
f = f0 + beta*y + ..... (higher order terms)
with: f0 = 2*Omega*sin(phi0)
beta = 2*Omega*cos(phi0)/R
y = the local north coordinate
On the northern (southern) hemisphere f0 is positive (negative);
beta is always positive.
In the absents of any bottom topography, the value of f0 is unimportant: it is a constant and drops out of the equations. Then the so-called beta-effect is the dominating term and this causes a cyclonic (anti-cyclonic) monopolar vortex to move to the north-west (south-west) on the northern hemisphere, as seen in the example above.
The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me