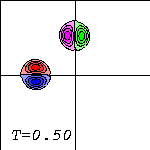
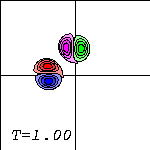
(You can click on an image for a somewhat larger version;
each is about 3.2 kb.)


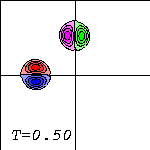
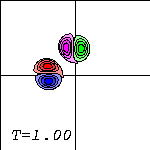
(You can click on an image for a somewhat larger version;
each is about 3.2 kb.)
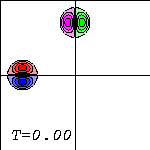
Two Lamb dipoles are initially (left picture) placed in the domain, one with its axis along the x-axis and the other with its axis along the y-axis, in such a way that they move towards each other (centre): the top half of the left dipole (coloured red) has positive vorticity and the bottom half (blue) negative, and the right half of the top dipole (green) has positive vorticity and the left half (magenta) negative.
The top (red) half of the left dipole feels the other dipole more than the bottom (blue) half does: the red half starts deforming and some of its vorticity gets in front of the blue half. Similarly, some of the vorticity of the left (magenta) half of the top dipole moves in front of the right (green) half. This can be seen somewhat in the centre picture, but more clearly in the right one.
The dipoles then get closer to each other (left). The red half of the left dipole and the magenta half of the top dipole get eventually so close (centre) that they are closer to each other than to their original partners. At that moment these two form a dipole which moves away from the collision site to the upper-left corner (right), leaving some of their vorticity behind at their original partner: there is some red (positive vorticity) drawn around the blue (negative), and some magenta (negative) around the green (positive).
While the newly formed dipole, which is small and compact, moves further
and further away rom the collision site, the vorticity left behind gets
wrapped all around the original partners (blue and green). These started as
half circles but have become more or less round: they are monopoles with
oppositely singed vorticity getting wrapped around them.
The whole structure now forms a large dipole
moving to the lower right corner, but since the dipole halves are
partly shielded by oppositely signed vorticity (from their old partners),
this dipole does not move very fast.
This row of pictures furthermore shows that fluid from outside the dipoles
in entrained ("absorbed") by the large dipole moving to the lower-right
corner as the oppositely signed vorticity gets wrapped around the original
partners: there are areas of white inside the dipole.
The motion of the dipole halves can also be seen in the next graph.
Trajectories of tracers initially placed at the extrema of vorticity (the "centra" of the dipole halves). The arrows indicate the initial direction of motion. Squares show the positions at T=0,50,100,...,350,400.
The motion of the Lamb dipoles is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units. What you see in the simulation above are lines of tracers: passive 'particles' that advection by the motion. In this particular case, the tracers are placed on streamlines of the Lamb dipole.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me