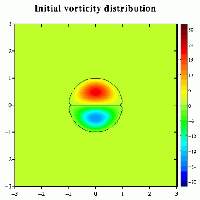
(You can click on an image for a somewhat larger version;
size: 30-45 kb.)

The boundary condition of no-slip walls implies that fluid cannot go through the wall, and cannot move along the wall: the velocity of the fluid is equal zero at the wall. Under this boundary condition vorticity inside the domain induces oppositely signed vorticity at the walls. This "extra" vorticity of course influences the evolution of the vorticity in the domain.


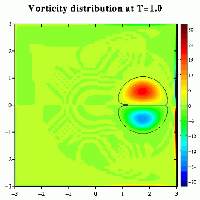
(You can click on an image for a somewhat larger version;
size: 30-45 kb.)
The Lamb dipole is initially placed at the centre of the domain
and moves to the right.
In the mean time oppositely signed vorticity is generated at the walls.
Colours represent the same vorticity values throughout the evolution.
The solid lines mark the vorticity area of the initial two dipole halves.
When the dipole reaches the wall it splits in two halves, like it does when it hits a stress-free wall. In this case, however, the halves interact with the wall induced oppositely signed vorticiy and two dipolar vortices are formed.
These "new" dipoles are asymmetric and therefore follow a curved path
as they move away from the wall.
The two dipoles will meet again on the line in the middle (along which
the original dipole initially moved).
These two dipoles then collide and the exchange partners
(see Collision of two Lamb dipoles) and
two new dipoles are formed, one moving to the right and another (smaller)
one moving to the left, until the reach the walls and interact with
the wall induced vorticity, ... etc.
The motion of the Lamb dipole is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units. Viscous effects are included in this computation, so that the vorticity levels gradually decrease as time goes on.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me