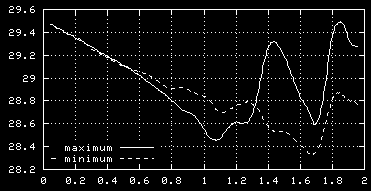
The maximum and -minimum of vorticity as
function of time (averaged over 20 time steps).
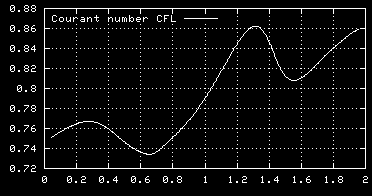
The Courant number CFL, a measure for the
maximum velocity in the domain, function
of time (averaged over 20 time steps).

Initialisation
Monopole: Bessel monopole of radius 0.5 centred at (0,0)
and strength (=circulation) :+4 or +8
==> extremum of initial vorticity:
+11.8 or +23.6
Dipole: Lamb dipole of radius 0.75 and velocity +2
centred at (-2,0) or (-2,+0.5)
==> extrema of initial vorticity: +/- 29.5
circulation per dipole half : +/- 10.2
Tracers: tracer contours:
- monopole: at radii 0.2 0.35 and 0.5
- dipole: at vorticity levels 0.01, 10 and 20
single tracer points:
- monopole: at the centre
- dipole: at the extrema of vorticity
Computation: domain: X = (-3, ..., 3), Y = (-3, ..., 3)
no. of grid points from wall to wall: (257, 257)
boundary conditions: stress-free along all walls
standard Arakawa scheme used
rotation effects: none
bottom topography: none
solver for streamfunction: FACR
viscosity: nu = 10^-3 (i.e. Re=1000 at T=0)
time step: dt = 0.0025
final time: T = 2 [800 time steps]
Some other graphs
For the main run of a weaker monopole and a head-on encounter:


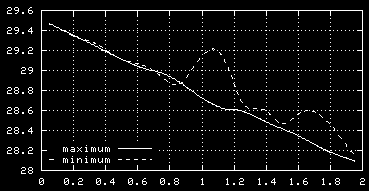
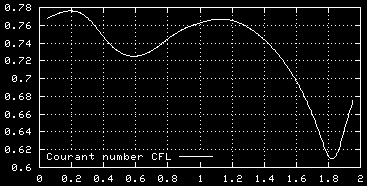
See the top of this page for links back.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me