<=== Jules Verne hoofdpagina

Het coderingsrooster van Mathias Sandorf
Jos van Geffen

In het eerste hoofdstuk van "Mathias Sandorf" onderschept de schurk van het verhaal een gecodeerde boodschap. In de Elsevier-uitgave van 1915 staat die boodschap aldus weergegeven:

 ghfhna      dalant      ltenka
 aohhzk      aenzse      tsnivi
 rnryoo      tnpees      seyehe
 lxosde      soelnl      sglpte
 veknni      ilarna      lotasa
 yareah      uezmtl      rradae

waarbij de drie "y" hierboven in het boek de combinatie "ij" is en een enkele letter voorstelt (Elsevier vertaalde de boodschap in het Nederlands). Deze gecodeerde boodschap is ontstaan uit een reguliere tekst met behulp van een 6-bij-6 rooster. In hoofdstuk vier wordt dat rooster gevonden en het ziet eruit zoals hieronder is weergegeven: een vierkant van 6-bij-6 vakjes met daarin 9 openingen, en aan een zijde een markering.

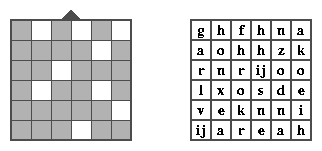
Door nu de letters per blok van 6-bij-6 op dezelfde afstanden te schrijven, zoals in het vierkant hierboven, en het rooster daarop te leggen worden 9 letters leesbaar, die in de normale leesvolgorde opgeschreven worden. Dan wordt het rooster een kwartslag rechtsom gedraaid en volgt een tweede set van 9 letter, etc. Voor het eerste tekstblok levert deze decodering:

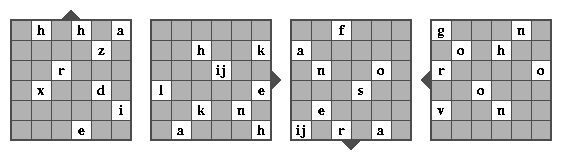
De andere twee blokken code worden op dezelfde manier behandeld en de oplossing is dan een reeks van letters. Die reeks blijkt achterstevoren gelezen te moeten worden. Voorzien van interpunctie ziet het bericht er dan aldus uit:

Alles is klaar. Op het eerste sein dat gij van Triëst zendt, zullen allen
als een man opstaan voor Hongarijes onafhankelijkheid. Xrzahh.

(waarbij de laatste zes letters ter opvulling zijn).

Over deze coderingswijze schrijft Verne in hoofdstuk twee dat het gebruik van zo'n roostersysteem de beste en veiligste manier is om een onoplosbaar geheimschrift te verkrijgen (mits het rooster geheim blijft, uiteraard).

Verne is hiermee wel wat erg optimistisch!

Omdat het 6-bij-6 rooster, met dus 36 vakjes, viermaal gedraaid wordt moet het 9 openingen hebben. Het aantal unieke mogelijkheden om deze 9 openingen over het 6-bij-6 rooster te verdeling is vrij groot, maar ook weer niet zo erg groot: 262.144. Iemand die het klaar zou spelen om in continue-dienst elke minuut een rooster uit te proberen is 4369 uur en 4 minuten bezig, oftewel 182 dagen, 1 uur en 4 minuten. Als het dus nodig zou zijn om zo'n botte probeer-methode te gebruiken, dan is dat alleszins haalbaar, zelfs in Verne's tijd. Het feit dat de boodschap van achter naar voren gelezen moet worden maakt het oplossen ervan nauwelijks moeilijker.

Maar het met botte kracht oplossen van een gecodeerd bericht is meestal de minst slimme aanpak, tenminste als het gaat om een betekenisvol bericht, bestaande uit betekenisvolle woorden, zoals in dit geval. Met wat statistiek en logisch nadenken over mogelijke lettercombinaties is het codebericht vrij makkelijk te ontcijferen. Hoe dat gaat wordt uitgebreid uit de doeken gedaan door Klaus Pommerening van de Johannes Gutenberg Universiteit in Mainz (Duitsland) op deze Duits-talige webpagina, uitgaande van de originele Frans-talige versie van het codebericht. Overigens is Klaus Pommerening's keuze op een enkele plaats misschien wel wat erg gelukkig, maar ook met 2 of 3 drie doodlopende keuzes meer is het codebericht veel sneller op te lossen dan in 182 uur.

En dan nu een prijsloos quizje. Welke van de volgende 8 roosters zouden bruikbaar zijn voor het maken van een codebericht?

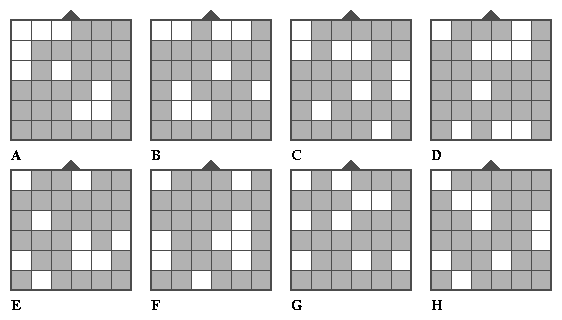
En welke van die bruikbare roosters is toegepast op de boodschap aan Graaf Sandorf met het volgende codebericht als resultaat?

 hfgnhk      aldnne      telkni
 hyazao      aetsae      neavts
 nhorlr      nzetsp      eihssy
 soexkd      lsloan      peegtt
 nieyor      naluez      saorla
 vnahea      irelmt      lareda

Om een bruikbaar 6-bij-6 rooster te hebben moeten de 9 openingen zodanig verdeeld zijn dat na viermaal draaien alle 36 vakjes precies eenmaal aan de beurt zijn geweest. Zoals gezegd levert dat voor de 9 openingen in het 6-bij-6 rooster in totaal 262.144 mogelijkheden op. Een 4-bij-4 rooster (met 4 openingen) heeft slechts 256 mogelijkenheden, terwijl een 8-bij-8 rooster (met 16 openingen) meer dan 4 miljard mogelijkheden heeft. Ook een vierkant rooster met een oneven aantal vakjes per zijde is uiteraard mogelijk, waarbij het middelste vakje niet gebruikt wordt.

Een vierkant rooster kan men zien als opgebouwd uit een aantal ringen met vakjes. Voor het 6-bij-6 rooster van Mathias Sandorf zijn er dat drie:

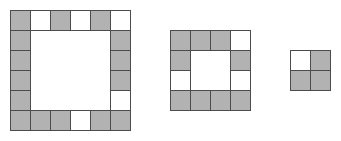
Voor deze ringen geldt van buiten naar binnen:
  *  de ring met N=6 vakjes per zijde heeft 20 vakjes, waarvan 5 open
  *  de ring met N=4 vakjes per zijde heeft 12 vakjes, waarvan 3 open
  *  de ring met N=2 vakjes per zijde heeft   4 vakjes, waarvan 1 open
In totaal dus 36 vakjes, met 9 openingen.

Om het aantal mogelijke unieke combinaties van openingen te bepalen is het belangrijk om in te zien dat de verdeling van de openingen langs de verschillende ringen onafhankelijk van elkaar is. Dat wil zeggen dat het aantal mogelijkheden per ring afzonderlijk bepaald kan worden, waarna de uitkomsten vermenigvuldigd worden om het totaal aantal mogelijkheden van het rooster als geheel te vinden.

Voor de ring N=6 zijn er 5 openingen en die kunnen op 1024 unieke manieren langs deze ring verdeeld worden. Voor de 3 openingen in de N=4 ring zijn er 64 mogelijkheden. En voor de N=2 binnenring met 1 opening zijn er vier mogelijkheden. In totaal dus 1024*64*4=262.144 mogelijkheden.

Met wat wiskunde kan het aantal mogelijkheden voor een willekeurig rooster opgeschreven worden. Een M-bij-M rooster heeft M*M vakjes, waarvan er M*M/4 open moeten zijn. Dat rooster is verdeeld in een aantal ringen met aan een kant N vakjes. Zo'n ring heeft in totaal 4(N-1) vakjes, waarvan er N-1 open moeten zijn. Het aantal unieke mogelijkheden om deze N-1 open vakjes langs de ring te verdelen is:

2^2(N-1) ,      N=1,2,3,4,...

Door nu de uitkomsten van de onderling onafhankelijke ringen van een M-bij-M rooster met elkaar te vermenigvuldigen volgt het totaal aantal mogelijkheden voor dat rooster. Het maakt hierbij uit of het om een even of oneven aantal vakjes per zijde gaat:

2^M*M/2 ,      M=2,4,6,...

2^(M*M-1)/2 ,      M=1,3,5,...

waarbij M=1 een niet erg zinvol rooster oplevert. Hierbij een tabelletje met wat getallen, links voor de afzonderlijke ringen, rechts voor roosters als geheel.

 N  per ring          M  gehele rooster
------------         -------------------
 1        1           1               1
 2        4           2               4
 3       16           3              16
 4       64           4             256
 5      256           5           4.096
 6    1.024           6         262.144
 7    4.096           7      16.777.216
 8   16.384           8   4.294.967.296

 

Oplossing van het quizje bruikbaar: A, C, F, G niet bruikbaar: B, D, E, H gebruikt voor codering: C

<=== Jules Verne hoofdpagina

 
Jos van Geffen -- Home  |  Site Map  |  Contact Me

created: 26 February 2005
last modified: 6 December 2012