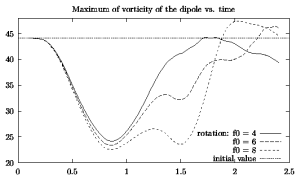
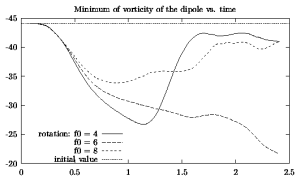
The positive half of the dipole is more or less restored for all three values of f0. The negative half is restored for f0=4 and 8 but torn apart for f=8.

Initialisation
Dipole: velocity: U = 2; maximum initial vorticity 44.25
radius: a = 0.5
angle of dipole axis with X-axis: 0 degrees
position: centre of the domain (-1.5,0)
Computation: domain: X = (-3, ..., 3), Y = (-3, ..., 3)
no. of grid points from wall to wall: (129, 129)
boundary conditions: stress-free along all walls
standard Arakawa scheme used
viscosity: nu = 10^-3 (i.e. Re=1000 at T=0)
time step: dt = 0.01
final time: T = 2.5
Background rotation: constant rotation f0 = 4, 6 and 8
Bottom topography: cosine ridge along the Y-axis:
fluid depth: H(X,Y) = 1.d0-A*cos(X*pi/w)-A
amplitude: A = 0.2 (max. height then 0.4)
width: w = 1.0
for: -w < x < +w
outside this region: H=1 (default fluid depth)
Tracers: along vorticity contours (i.e. along streamlines)
of the Lamb dipole at vorticity levels: 0.1
and a single tracers at each extremum
Some results
Here are the graphs for the maximum (left) and minimum (right)
vorticity as a function of time for the three rotation rates:


The positive half of the dipole is more or less restored for
all three values of f0. The negative half is restored for
f0=4 and 8 but torn apart for f=8.
<=== Lamb dipole crossing a ridge -- with background rotation
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me