Initialisation 
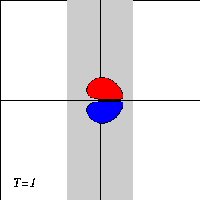
Dipole:      velocity: U = 2; maximum initial vorticity 44.25
             radius: a = 0.5
             angle of dipole axis with X-axis: 0 degrees
             position: centre of the domain (-1.5,0)
Computation: domain: X = (-3, ..., 3), Y = (-3, ..., 3)
             no. of grid points from wall to wall: (129, 129)
             boundary conditions: stress-free along all walls
             standard Arakawa scheme used
             no rotation effects included
             viscosity: nu = 10^-3 (i.e. Re=1000 at T=0)
             time step: dt = 0.01
             final time: T = 2.5
Bottom topography: cosine ridge along the Y-axis:
             fluid depth: H(X,Y) = 1.d0-A*cos(X*pi/w)-A
               amplitude: A = 0.2 (max. height then 0.4)
                   width: w = 1.0
                     for: -w < x < +w
             outside this region: H=1 (default fluid depth)
Tracers:     along vorticity contours (i.e. along streamlines) 
             of the Lamb dipole at vorticity levels: 0.1
             and a single tracers at each extremum

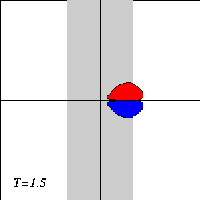
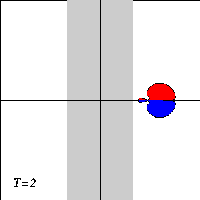
The tracers at the extrema of vorticity cross the left edge of the topography x=-1 at T=0.26, they cross the top x=0 at T=0.92, and the right edge x=+1 at T=1.55.

The evolution of the tracer contours looks like this:

(The initial situation is drawn in the left figure with a dashed line.)

The following plots show the maximum of vorticity as function of time and the surface of the tracer contour in the positive (upper) half of the dipole as function of time:

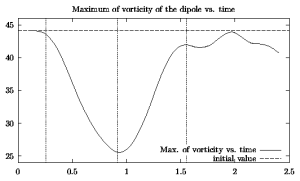
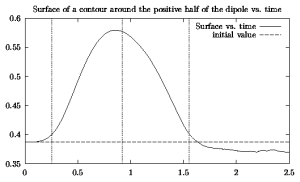
(The vertical lines in both graphs show the moments in time
when the dipole crosses the edges and the top of the ridge.)

Clearly visible is that when the dipole

 i) climbs the ridge, the vortex becomes weaker and bigger;

ii) descends the ridge, the vortex becomes stronger and smaller.

Notes:

• Viscosity is present in this computation, but the time span is so short that the effect of viscous decay is not observable.
• The right boundary is a stress-free wall: when the dipole hits it, it splits up (see Lamb dipole in a domain with stress-free walls); the start of this process is visible at about T=2.3.
• Vorticity contours in the plots on the main page are drawn at: +/- 0.1, 5, 10, 15, 20, 25, 30, 35, 40.

<=== Lamb dipole crossing a ridge

 
Jos van Geffen -- Home  |  Site Map  |  Contact Me

created: 11 July 1997
last modified: 26 May 2001