Lamb dipole in a domain with stress-free walls

Details on the computation and presentation 

Initialisation 
Dipole:      velocity: U = 2; maximum initial vorticity 22.1
             radius: a = 1  
             angle of dipole axis with X-axis: 0 degrees
             position: centre of the domain (0,0)
Computation: domain: X = (-3, ..., 3), Y = (-3, ..., 3)
             no. of grid points from wall to wall: (129, 129)
             boundary conditions: stress-free along all walls
             standard Arakawa scheme used
             no rotation effects included
             no bottom topography
             viscosity: nu = 10^-3 (i.e. Re=1000 at T=0)
             time step: dt = 0.01
             final time: T = 10
Tracers:     along vorticity contours (i.e. along streamlines) 
             of the Lamb dipole at vorticity levels: 0.1, 6.0, 
             12.0, 18.0; and a single tracers at each extremum
Some results 

Positions (X,Y) of the tracer at the maximum of vorticity in 
the 'corners' of its path, shown by the pictures; for the 
minimum they are mirrored in the Y-axis. 
Futher: D = distance traveled since previous point (assuming 
            a straight line)
        V = average velocity over that distance; see below

 NTIME    TIME         X           Y         D       V
    0  0.0000E+00  0.0000E+00  0.4805E+00    -       -
  147  0.1470E+01  0.2327E+01  0.6604E+00  2.4164  1.6438
  278  0.2780E+01  0.2326E+01  0.2330E+01  1.6696  1.2745
  431  0.4310E+01  0.5690E-02  0.2507E+01  2.3271  1.5209
  590  0.5900E+01 -0.2307E+01  0.2304E+01  2.3216  1.4601
  726  0.7260E+01 -0.2307E+01  0.7013E+00  1.6027  1.1785
  892  0.8920E+01 -0.4498E-02  0.5129E+00  2.3102  1.3917
The highest velocity is reached when the dipole halves are semi-circular. The velocity is lowest in the corners. This can also be seen from this graph: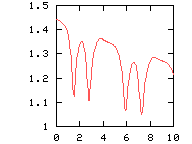
Courant number CFL as a function of time
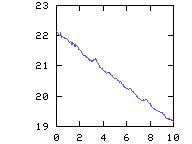since CFL is a measure for the maximum velocity on the grid. The overall velocity in that graph decreases in the course of time. This is caused by the viscosity: vorticity is spread over a larger area and the extrema of vorticity decrease in strength, which reduces the velocity of the vortex.
The effect of viscosity can also be seen in these pictures:
max. and -min. of vorticity, which overlap
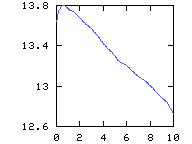pos. and -neg. circulation, which overlap
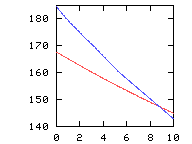energy*7(red) and enstrophy(blue)
all as a function of time (larger versions are about 2.8 kb).

Note

The tracer lines are not always smooth. The reason for this is that the representation of the lines by points is not always accurate enough. But since these tracers only passively follow the flow, this has no effect on the computations. It needs repair, though.

<=== Lamb dipole in a domain with stress-free walls

 
Jos van Geffen -- Home  |  Site Map  |  Contact Me

last modified: 26 May 2001