Bessel monopole encounters a north-south ridge -- f0=0

Bessel monopole encounters a north-south ridge
`f0`=0: equatorial case

A monopolar vortex, such as the Bessel monopole, will move in the presence of a background rotation, due to the Coriolis force, as explained on the page about a Bessel monopole on a beta-plane. The rotation effects are described in the model with the Coriolis parameter f=f0+beta*y. The value of f0 does not matter for that simulation since there is no bottom topography example. If there is a bottom topography, then things can be quite different.

In the simulations presented here the monopole encounters a north-south oriented ridge, as it travels to the north-west due to the beta-effect.

Simulation

Consider first a case in with f0 is absent, but with a bottom topography: a ridge along the y-axis, i.e. a north-south ridge. The cross-section of this ridge is a full cosine. The height of the ridge at the centre is h_max=0.4 and it lies between x=-1 and x=+1 (named: w=1). The rest of the initial situation is the same as for the Bessel monopole on a beta-plane.

Contours of relative vorticity of the initial situation.
The location of the ridge is shown by the shaded region.
(You can click on the pictures for a larger version.)

For all graphs: positive contours (0.1 to 2.0 at an interval of 0.1) are drawn solid, negative contours (-0.1 to -2.0 at an interval of -0.1) are drawn dashed, and the zero contour is dotted. Since the maximum of vorticity at the centre of the monopole is much larger than 2.0, the vortex looks like a "hole".
Note that the domain measures 20 by 20 length units -- the graphs show only the central part of this domain.

Turning on the time evolution means that the monopole moves to the north-west, due to the beta-effect, and it encounters the ridge:

The monopole then starts climbing the ridge. But the effect of the topography is quite strong and the monopole moves along the ascending (east) side of the ridge to the north, while it is being deformed heavily:

Eventually there is again a clear vortex on the west side of the top of the ridge and after this vortex has descended the ridge it continues it beta-induced motion to the north-west:

This MPEG movie (0.5 Mb; 101 frames) featuring the evolution from T=0 until T=50, shows far more clearly the effect of the ridge on the monopole.
There is also a colour version of the MPEG movie, which is nice to look at but shows the Rossby waves less clear.

As the monopole moves, it leaves behind vorticity in the form of so-called Rossby waves, and the monopole interacts with this vorticity again, leading to a non-straight motion to the north-west. When the monopole has reached the ridge, it starts moving more to the north than it would have done without the ridge (cf. the page on the Bessel monopole on a beta-plane) and at the same time the vortex becomes weaker (as explained on the page about the effect of a bottom topography). For this simulation:

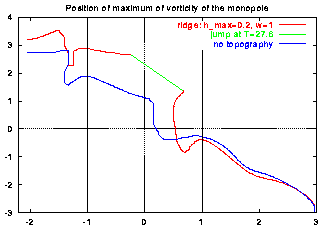
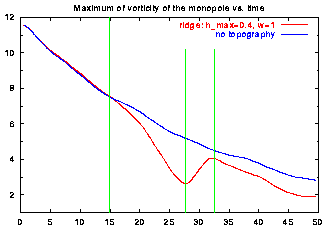
Motion of the maximum of vorticity of the monopole crossing a ridge (red) and in the case of no topography (blue). The think vertical lines indicate the edges of the ridge.
: Maximum of vorticity versus time of the monopole crossing a ridge (red) and in the case of no topography (blue). The green lines indicate the moments in time when the maximum of vorticity crosses the edges and the top of the ridge.

As the monopole moves to the north on the east side of the ridge it is deformed (see above) and partly crosses the top of the ridge. During this time the maximum of vorticity is located to the right of the top. At a certain moment the part of the vortex to the left of the top becomes the strongest one and then the maximum of vorticity is "suddenly" located there. That is the origin of the "jump" in the monopole's trajectory, shown in green in the left graph. This is the moment when the maximum of vorticity reaches a minimal value in the right graph.

Non-zero Coriolis constant `f0`

In the above simulation the constant f0 in the Coriolis parameter equals zero. This means, actually, that the ridge is situated at the equation, f0=0 there.

For a monopole on a pure beta-plane the value of f0 does not matter. In this case, however, there is a bottom topography present, and a non-zero value has effect on the monopole's evolution. Positive f0-values mean that the ridge is on the northern hemisphere, and for negative f0-values the ridge is on the soutern hemisphere.

For f0-values near f0=0 the effect is not very big, depending on the height of the ridge, but for larger absolute f0-values the effect is considerable. These two example show this clearly:

===> Bessel monopole encounters a north-south ridge -- with f0=+3.
===> Bessel monopole encounters a north-south ridge -- with f0=-3.

For details on simulations with different f0-values and heights, see:: Van Geffen, J.H.G.M. and Davies P.A.: 1999,
"A monopolar vortex encounters a north-south ridge or trough,"
Fluid Dynamics Research, in press.

Effect of nature of the ridge

The effect the ridge has on the monopole's evolution evidently depends on the nature of the ridge: its orientation, height and width. Some remarks on this may be in order:

Since the method assumes that the motions are two-dimensional (2D), the ridge cannot be too heigh. Above h_max=0.4 is used -- this is probably the height acceptable ridge in a 2D model.
The higher the ridge, the stronger the deformation of the monopole, which is to be expected.
For h_max<0 the topography is a trough rather than a ridge of course. In that case the effect of the topography is roughly the same, "mirrored" in the no-topography case.
The effect of the width of the ridge is less clear to describe. A very narrow ridge has hardly any effect. For a ridge of half the width of the above (w=0.5), the monopole is split in two and looks somewhat like the w=1 case above. For w=0.75 there is no splitting in two, neither is there for w>1. Ridges with w>1.5 seem to be too wide for the monopole to cross: due to viscous effects and the loss of vorticity to Rossby waves, the monopole is too weak when it is at the ridge, to get free of it and it decays at the ridge.
A north-south ridge, like in the simulation shown above, has considerably more effect on the fate of the monopole than an east-west ridge. The reason for this is that a north-south ridge deforms the potential vorticity field of the rotation much more than an east-west ridge. The next three graphs show this difference.

Contours of potential vorticity, drawn at the same levels as the contours above, for the case of no topography (left), an east-west ridge (middle) and a north-south ridge (right). The latter ridge obviously deforms the potential vorticity from the pure beta-effect (left) more than the east-west ridge does. For the pure beta-effect, the contours are straight lines, since the potential vorticity then equals beta*y (=0.3*y in this case).
The monopole shows up again as a "hole" at (+3,-3).

For details on simulations with different orientation, height and width, see:: Van Geffen, J.H.G.M. and Davies P.A.: 1999,
"Interaction of a monopolar vortex with a topographic ridge,"
Geophys. & Astrophys. Fluid Dynamics 90, 1--41.

The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.

===> Some details on the computation presented on this page for those who are interested.

<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.

Jos van Geffen -- Home | Site Map | Contact Me