The basic effects of the ridge on the dipole are explained on a page about the Lamb dipole crossing a ridge without background rotation: the dipole becomes weaker and wider as it climbs the ridge. This will also take place when there is a background rotation, but the rotation affects the motion too when the dipole climbs the ridge, since (in the absence of viscosity):
vorticity + rotation
---------------------- = constant
fluid depth
Consider now a constant rotation f, then it is clear from this that
the vorticity values of the two dipole halves are affected differently:
the positive half becomes weaker than the negative half. A simple
example with numbers show this clearly for a rotation of 4 and
an initial vorticity value of 20:
fluid depth = 1 fluid depth = 0.5
Constant A = 24 = (+20 + 4) / 1 = ( +8 + 4) / 0.5
Constant B = -16 = (-20 + 4) / 1 = (-12 + 4) / 0.5
Both dipole halves are of equal strength when the fluid depth is 1 (the
default value). At fluid depth 0.5, the negative half has a strength of
of -12 and the positive half of +8, hence the negative half is stronger
then the positive half.
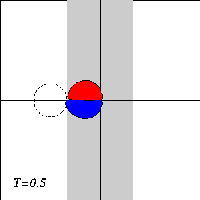
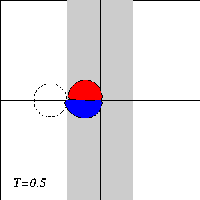
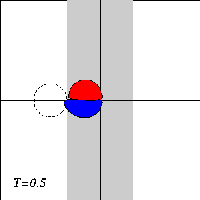
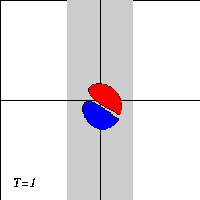
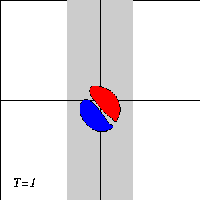
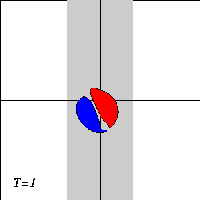
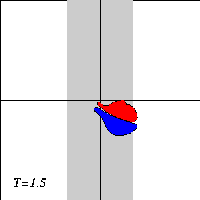
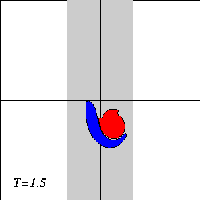
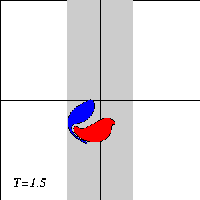
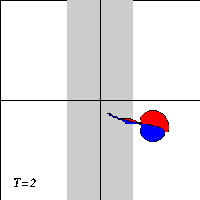
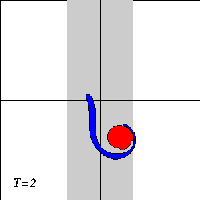
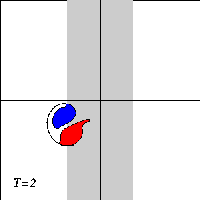
A dipole with two halves of unequal strength -- a so-called asymmetric dipole -- will move along a curved path, with the strongest half on the inside of the curvature. When the dipole climbs the ridge in the presence of a background rotation, it will therefore bend towards the negative half. And when the dipole descends the ridge again, the dipole will bend towards the positive halve.
Due to the asymmetry of the problem, however, the dipole will not return to its initial line of motion when it leaves the ridge: since the dipole looses vorticity as it moves, the two dipole halves are of unequal strength when the dipole leaves the ridge, and it will be an asymmetric dipole moving along a curved trajectory.
What actually happens to the dipole depends on the strength of the background rotation: a weak rotation will deflect the dipole from its straight trajectory. whereas a strong rotation can reflect the dipole backwards. For intermediate rotation values, the dipole can be torn apart.
Here are three typical cases, with time increasing downward:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Evolution of tracer contours placed initially on the edge of a Lamb dipole (indicated by a dashed line in the figures of the top row) as the dipole moves for three different values of the background rotation: weak, intermediate, and strong, respectively. | ||
The motion of the Lamb dipole across the ridge is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units. What you see in the simulations above are lines of tracers: passive 'particles' that advection by the motion. In this particular case, the tracers are placed on streamlines of the Lamb dipole.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
Jos van Geffen --
Home |
Site Map |
Contact Me