The Lamb dipole
The Lamb dipole is a dipolar vortex structure with
a continuous vorticity distribution within a circular region.
This dipole moves along a staight line
with a constant velocity and without change of form.
It is a stationary solution of the two-dimensional vorticity equation
(Navier-Stokes equation) when there are no viscous effects and the
domain is infinite.
When viscous effects play a role, the vorticity is spread
over a larger area and the dipole decreases in strength, so that the
velocity also decreases in the course of time; the motion remains
along a straight line though.
In case the domain is finite, the velocity of the dipole is less
than in an infinite domain.
A somewhat more precise description
The Lamb dipole has a continuous vorticity distribution within
a circle of radius a.
Inside this circle there is a linear relationship between the
vorticity omega and the streamfunction psi, namely:
omega=k2psi, where k is a constant
given by ak=3.83.
Outside this circle there is no vorticity: omega=0.
The flow outside the dipole is a potential flow:
a two-dimensional flow around a circular cylinder placed in a flow field
with a uniform velocity U0, as sketched below.
-
-
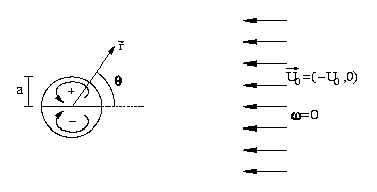
Schematic representation of a Lamb dipole of radius a in a
uniform flow field, with no background rotation.
The line theta=0 is the dipole's axis along which it moves.
As indicated in the figure above, one half of the dipole has positive
vorticity, whereas the other half has negative vorticity.
The total circulation, that is the 'sum' of all vorticity, equals zero.
This can also be seen in the following pictures.
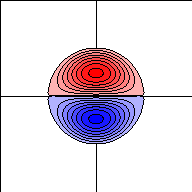
Left: A plot of the streamlines of the Lamb dipole, which
coincide with contours of vorticity. The horizontal line is the dipole
axis, the vertical line is the line through the extrema of vorticity.
The dipole was initialised in a 4x4 domain with radius 1 and
velocity 2. The levels of vorticity in the left picture are from
0 to 21 with step 3; the maximum is 22.1.
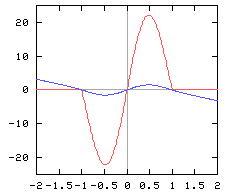
Right: Profile of vorticity (red) and streamfunction (blue)
along a line through the extrema of vorticity.
Within the dipole, the fluid flows along the streamlines, around the
extrema of vorticity, as indicated by the round arrows in the top figure.
This means that the largest velocity (in the positive x direction)
occurs at the dipole axis, as the graph below shows.
The velocity of the dipole as a whole is the velocity at the
extrema of vorticity (which are at y equal 0.48 and -0.48): 1.575,
indicated by the blue horizontal line.
Left:
Profile of the velocity in the positive x-direction (red)
along a line through the extrema of vorticity.
The velocity of the dipole as a whole is 1.575, indicated by the blue line.
(Due to the finiteness of the domain, the velocity of this dipole
is less than the value of U0=2 it is initiated with.)
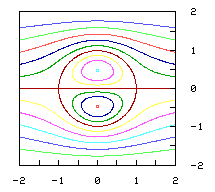
Right:
Plot of the streamlines inside and outside the dipole.
The levels are -2.5 to 2.5 with step 0.5; cf. the profile in the
graph above.
Chaplygin's work on dipoles
The Lamb dipole is named after Sir Horace Lamb who in the second
edition of his treatise Hydrodynamics (1895) considered
this solution in a rather sketchy way, without giving details.
In the third edition of 1906 Lamb gives some more details, thus
really describing the dipole solution.
Resently, work of the Russian scientist S.A. Chaplygin has been
rediscovered, showing that Chaplygin discussed dipole solutions
in a more general way, assuming that the linear relation between
vorticity and streamfunction is
omega=k2(psi-lambda),
where lambda is some constant.
Hence, the Lamb dipole is with lambda=0 a special case of the
'Chaplygin dipole'.
Chaplygin published his solution in 1903, i.e. before Lamb's
description was published.
See on this matter:
V.V. Meleshko and G.J.F. van Heijst,
"On Chaplygin's investigations of two-dimensional vortex structures
in an inviscid fluid," J. Fluid Mech. 272, 157-182, 1994.
<=== Numerical simulations of 2D vortex
evolution with a Finite Difference Method.
Jos van Geffen --
Home |
Site Map |
Contact Me
last modified: 26 May 2001
