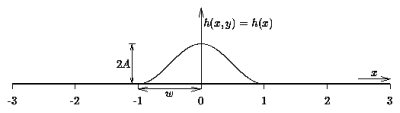
Cross-section of a cosine-shaped ridge along the y-axis and uniform in the y-direction. The maximum height of the ridge (at x=0) is 2A, and its width is w. In the example shown here A=0.2 and w=1.

The computation is actually purely two-dimensional, but introducing a third dimension for illustrative purposes only, a "cross-section" of the ridge looks like this:

The dipole is initially placed to the left of the ridge:
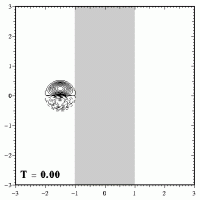
The dipole will now move to the right because of its self-induced motion and start climbing the ridge. The general effect of a bottom topography is that when a dipole climbs a ridge it will weaken and widen, since (in the absence of viscosity):
vorticity
----------- = constant (no background rotation)
fluid depth
Both dipole halves are affected in the same way by this topography effect
(provided there is no background rotation, as is the case here): both
halves become weaker as the fluid depth decreases.
Consider for instance a dipole with two halve of strength 20 at fluid depth
1 (the default value):
fluid depth = 1 fluid depth = 0.5
Constant A = 20 = +20 / 1 = +10 / 0.5
Constant B = -20 = -20 / 1 = -10 / 0.5
Both dipole halves have a strength of 10 at fluid depth 0.5.
This means that the dipole will not move away from the straight path it would follow if there was no topography. The weakening and widening of the dipole can be seen clearly in these plots:
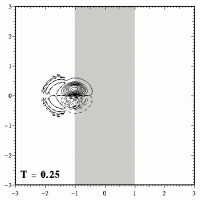
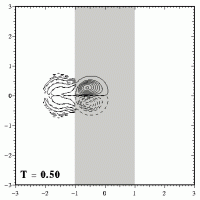
When the dipole has crossed the maximum height of the ridge (which is at x=0), it descends from the ridge. During that descend the dipole will shrink again and become stronger, as shown here:
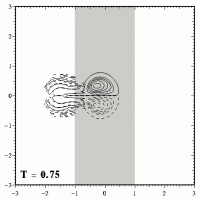
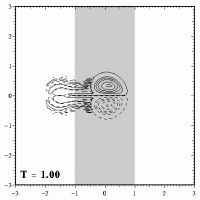
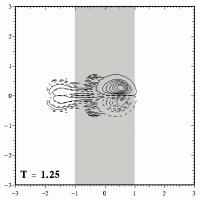
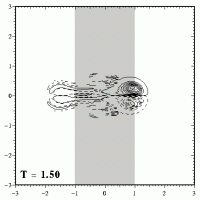
Once the dipole has left the ridge, the dipole has the same size and strength again, which it had before it started climbing the ridge. After leaving the ridge, the dipole will therefore move further to the right, like an undisturbed Lamb dipole does.
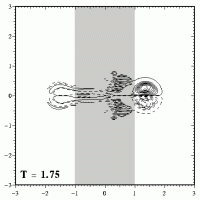
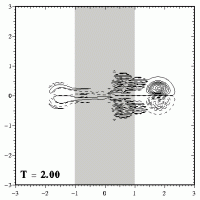
The motion across the ridge can be seen nicely in an MPEG movie (700kb; 126 frames), with the evolution until T=2.5, when the dipole has reached the right boundary.
See the page Lamb dipole crossing a ridge -- with background rotation about this.
The motion of the Lamb dipole across the ridge is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me