A tripolar vortex is a vortex consisting of three part: a centre part and two oppositely signed satellites. A symmetric tripole had no net linear momentum, so it does not move; if it is not symmetric, the tripole might be moving. The tripole does have a net angular momentum, as a result of which is rotates.

Tripolar vortices have been seen to emerge from 2D turbulence in laboratory experiments and in numerical experiments.

There is no mathematical equation that can describe the vorticity distribution of a tripole. It must result from another vortex that evolves due to nonlinear and viscous effects, as is the case in laboratory experiments. In such experiments the vortex starts as a monopole with a, say, positive centre and a ring of negative vorticity around it. This ring is under certain circumstances unstable and that can lead to the formation of two negative satellites. See for example these pictures, taken from an experiment by G.J.F. van Heijst (Eindhoven):

(GIF (118kb)  /  JPEG (28kb))

To make such a tripole appear from a simulation with my program, I started from the following vorticity distribution (which is, to be honest, not very physical, but together with viscosity and nonlinear effect, the whole thing turns out quite nice). A monopolar vortex is made with a positive centre, then a small ring of zero vorticity, and then a broader ring of negative vorticity. Outside this vortex, there is no vorticity. The vorticity profile along the x-axis looks like the picture on the left here:

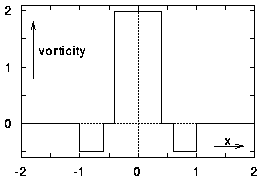
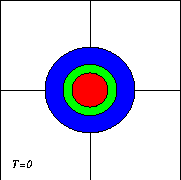
If the monopole is made exactly circular, then all it does is rotate. To get a tripole, it must be slightly eccentric. The picture on the right shows the initial situation "from above": the vortex is somewhat squeezed in the y-direction (eccentricity: 0.95). The red centre has positive vorticity, the green ring zero, and the outer blue ring negative.

The next thing to do is to turn on the evolution and see what happens. First of all the monopole will rotate anti-clockwise, because the centre of the vortex has positive vorticity (it is cyclonic):

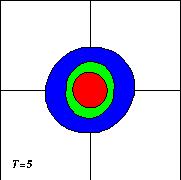
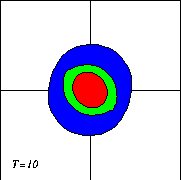
And clearly the vortex starts deforming. As time goes on this deformation grows:

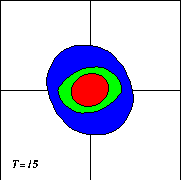
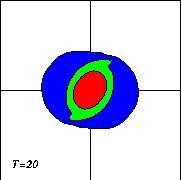
And a tripolar vortex emerges! Further evolution lead to a clearer "separation" of the satellites form the central core:

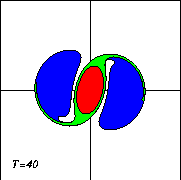
But since the tripolar vortex is a coherent, stable structure in 2D turbulence -- that is why it emerges from 2D turbulence in the first place! -- the satellites remain close to the core and the tripole will continue to rotate. Due to viscous effects the tripole will gradually decay, but that is another story.

The whole evolution, until T=50, is available as an MPEG movie (101 frames, 568 kb) with pictures every 0.5 time units, against a nice black background.

Viscosity does of course play a role in the evolution: is smears out the vorticity and helps in the formation of the tripole. If you are wondering what the vorticity profile looks like, here it is at T=50 along line (approximately) through the extrema of vorticity:

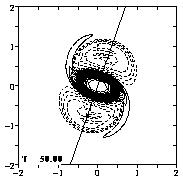
On the right you see contours of vorticity at T=50 and the line along which the profile is given. Clearly the vorticity is not yet fully a nice continues function, and hence the formation of the tripole is not really complete yet, but it is not far from it.

Some further notes

• The value of the vorticity of the centre is initially such, that the total circulation equals zero.
• To minimise unwanted effects of the boundary of the computational domain, the boundaries are at -5 and +5 on either side; the part of the domain shown ranges from -2 to +2.
• A computation with a Contour Dynamics Method looks very similar; see the movie at this page.
• Using piecewise uniform vortices, as done above, is physically not really realistic, but it nicely illustrates what happens. A physically more realistic way of obtaining a tripolar vortex is using a shielded exponential vortex which is made slightly elliptic, as done by Carton et al. (1989, Europhys. Lett., vol. 9, pp. 339-344).
• The larger the eccentricity is, the faster the formation of the tripole sets in, as can be expected. Compare, for example, the situation at T=20 from the above case of eccentricity 0.95 with the cases 0.9 and 0.8:

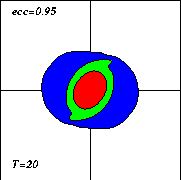
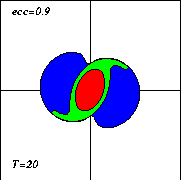
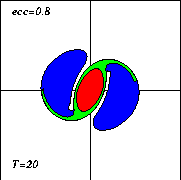
The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units. What you see in the simulation above are lines of tracers: passive 'particles' that advection by the motion; initially they are placed along the elliptical edges of the vorticity areas.

===> Some details on the computation presented on this page for those who are interested.

<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.

 
Jos van Geffen -- Home  |  Site Map  |  Contact Me

created: 16 February 1998
last modified: 26 May 2001