(You can click on an image for a somewhat larger version;
each is about 2.5 kb.)

The boundary condition of stress-free walls implies that fluid cannot go through the wall, but can move freely along the wall. In physical terms: the velocity of the fluid perpendicular to the wall is zero, whereas the velocity tangential to the wall is undetermined. A vortex reaching such a boundary sort of 'feels' its reflection in the wall and interacts with it.



(You can click on an image for a somewhat larger version;
each is about 2.5 kb.)
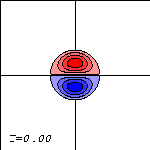
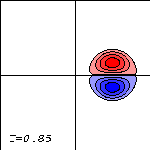
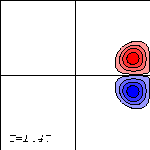
The Lamb dipole is initially placed at the centre of the domain (left) and moves to the right (centre). After a while it reaches the right wall (right).
Due to the stress-free condition on this boundary the dipole splits in two halves, which move along the wall in opposite directions (left). It is as if the dipole collides with its reflection in the wall and the behaviour is the same as that of a head-on collison of two Lamb dipoles. When the dipole halves reach the corners of the domain (centre) a similar 'collision' with a mirror-dipole takes place and the halves continue there way along the top and bottom walls (right).
In the next corner (left) there is again a 'collision' with a mirror-dipole and the halves move along the left wall (centre), until the reach each other (right) and the halves join to form a complete dipole again.
This dipole then again moves to the right (left) until it has reached the centre of the domain again (centre). Now the cycle can start all over again (right).
Viscous effects are included in this computation, so that the dipole becomes bigger in the course of time, as can for instance be seen from the path of the extrema of vorticity of the dipole:
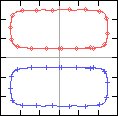
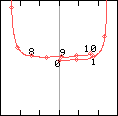
left:
Path of a passive tracer placed at the extrema of vorticity
from T=0 to T=10. The domain is from -3 to +3 in both x and y direction.
Marks on the lines are shown every 0.5 time units.
right:
Magnification of a part of the path of the tracer on the maximum of
vorticity; the y direction is from 0 to 1 only.
Numbers give moments in time.
When the tangential velocity is also zero, the boundaries are called no-slip walls. A simulation of a Lamb dipole in a domain with no-slip walls therefore leads to a very different behaviour.
The motion of the Lamb dipole is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units. What you see in the simulation above are lines of tracers: passive 'particles' that advection by the motion. In this particular case, the tracers are placed on streamlines of the Lamb dipole.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me