
A dipole encounters a monopole
monopole weaker / encounter with offset
A Lamb dipole with radius 0.75 and
velocity of +2 (i.e. moving to the right) is placed to the
left of a positive Bessel monopole
with radius 0.50 at the origin.
In the main run of this example the
dipole is along the x-axis, making the encounter head-on, and
the monpole has a circulation of +4, which means that the monopole is
weaker than each dipole half.
In this example:
-
The circulation of the monopole is +4, which makes the monopole
weaker
than each dipole half, since the circulation per dipole half is about 10.2.
-
The dipole is located 0.5 above the x-axis:
the encounter is with an offset.
The initial situation is shown in the following two graphs:
-
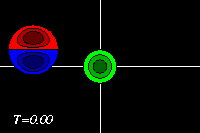
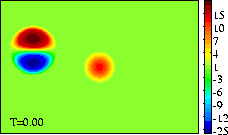
-
Initial tracer (left) and vorticity (right) distribution.
The domain shown is x=[-3.0:+3.0], y=[-2.0:+2.0].
The extrema of voriticity are +/- 29.5 for the dipole
and +11.8 for the monopole.
The monopole has an angular momentum: it rotates about its central point,
without moving.
The dipole has a linear momentum: it moves in the direction of its axis, in
this case to the right, towards the (weaker) monopole.
The monopole rotates counter-clockwise, like the top half of the dipole.
The result of the rotation is that the dipole is pushed down, to negative
y-values, while it moves towards the monopole, like in the
main run without offset. But since the
dipole now starts at a higher initial y-value, the dipole reaches the
monopole with its negative half, rather than with its positive half.
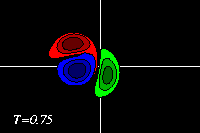
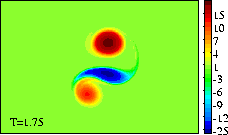
This can be seen clearest in the tracer plots:
-
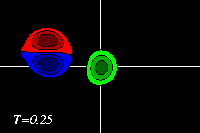
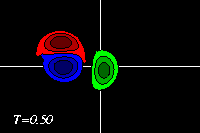
The negative dipole half (blue) then forms with the positive
monopole (green) a dipolar structure.
Since the monopole is weaker than the dipole half, the newly formed dipolar
structure will move along a curved path, with the stonger half on the
inside.
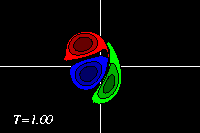
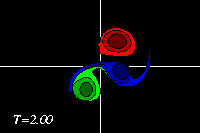
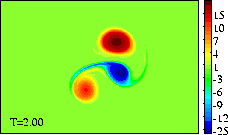
Meanwhile the original positive dipole half (red) is not a monopole, which
does not move on its own (there is a small motion, due to the dipolar
structure close by):
-
-

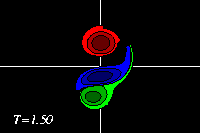
The curved path of the dipolar structure brings the negative dipole half
back close to its former positive and equally-strong partner.
Their combination is so strong that the negative dipole half teams up again
with its former partner to form a dipole. This dipole then moves away again
from the weaker positive monopole. Due to the interaction, however, there is
some shedding for vorticity and the monopole (green) has a small patch of
negative vorticity (blue) from the dipole.
-
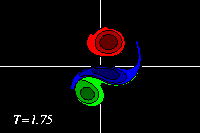
-
-
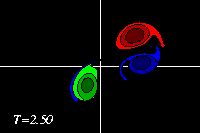
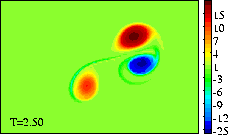
In the main run without offset the monopole
merges with the dipole into a new, a-symmetric dipole.
In this example there is an "exchange of partners", but this is only
temporarily, because the monopole is weaker than the dipole.
If this simulation is done
with a monopole that is nearly as strong as the
dipole, then the "exchange of partners" is permanent: the dipole moves
away to negative y, leaving the original positive dipole half (red)
behind as a monopole.
-
These MPEG movies (101 frames; 568kb) show the evolution until T=2.5
more clearly:
-
===>
MPEG movie of the tracer distribution
-
===>
MPEG movie of the vorticity distribution
At initialisation, a single tracer particle was placed at the extrema of
vorticity of both vortices. The next graph shows their trajectories:
-
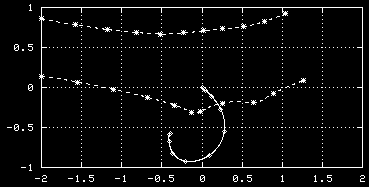
-
Trajectories of the tracers, initially placed at
the extrema of vorticity of the monopole (solid
line) and the dipole (dashed line).
Symbols are placed at intervals of T=0.25.
Some further remarks
See the main run of this example,
with a weaker monopole and a head-on encounter.
The evolution of the vorticity distribution is computed with a
Finite Difference Method
which solves the two-dimensional vorticity (Navier-Stokes) equation.
Time and distances are given in dimensionless units.
===> Some details on the computation presented
on this page for those who are interested.
<=== Numerical simulations of 2D vortex
evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me
created: 20 September 1999
last modified: 26 May 2001















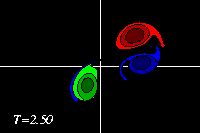


 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me