A dipole encounters a monopole

monopole nearly as strong / encounter head-on

 
A Lamb dipole with radius 0.75 and velocity of +2 (i.e. moving to the right) is placed to the left of a positive Bessel monopole with radius 0.50 at the origin.

In the main run of this example the dipole is along the x-axis, making the encounter head-on, and the monpole has a circulation of +4, which means that the monopole is weaker than each dipole half.

In this example:

The initial situation is shown in the following two graphs:
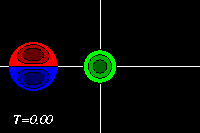
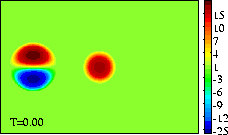
Initial tracer (left) and vorticity (right) distribution.
The domain shown is x=[-3.0:+3.0], y=[-2.0:+2.0].
The extrema of voriticity are +/- 29.5 for the dipole
and +23.6 for the monopole.
The monopole has an angular momentum: it rotates about its central point, without moving. The dipole has a linear momentum: it moves in the direction of its axis, in this case to the right, towards the monopole.

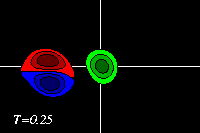
The monopole rotates counter-clockwise, like the top half of the dipole. The result of the rotation is that the dipole is pushed down, to negative y-values, while it moves towards the monopole, like in the main run without offset. Since the monopole (green is in this example stronger, the deformation of the positive dipole half (red) is larger and the dipole is pushed further to negative y-values. This can be seen clearest in the tracer plots:

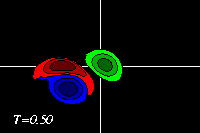
Due to the approach of the dipole, the monopole is deformed slightly and pushed away from its initial location. The deformation of the positive dipole half (red) continues and it effectively is squeezed against the positive monopole (green) and the two form a positive vorticity patch, and a new dipole is formed:
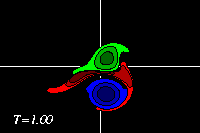
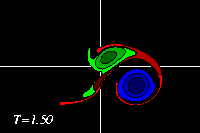
The original positive dipole half (red) is entirely torn apart in this proces: part of its vorticity is around the original positive monopole (green), part is around the negative dipole half (blue), and part is in a vorticity tail, which also contains some of the vorticity from the original monopole:
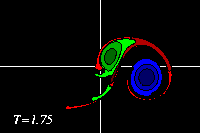
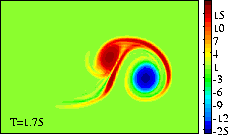
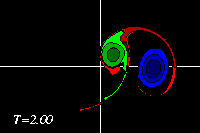
The dipolar structure thus formed is evidently a-symmetric, so that it follows a curved path, leaving behind a tail of vorticity. The dipolar structure thus formed is clearly not very tight, but as there is no other vortex present it will move as a dipole. Since it is a-symmetric, the path it follows is curved.

These MPEG movies (81 frames; 456kb) show the evolution until T=2 more clearly:
===> MPEG movie of the tracer distribution
===> MPEG movie of the vorticity distribution

 
At initialisation, a single tracer particle was placed at the extrema of vorticity of both vortices. The next graph shows their trajectories:

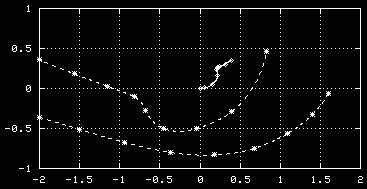
Trajectories of the tracers, initially placed at
the extrema of vorticity of the monopole (solid
line) and the dipole (dashed line).
Symbols are placed at intervals of T=0.25.

 
Some further remarks

See the main run of this example, with a weaker monopole and a head-on encounter.

The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.

===> Some details on the computation presented on this page for those who are interested.

<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.

 
Jos van Geffen -- Home  |  Site Map  |  Contact Me

created: 21 September 1999
last modified: 26 May 2001