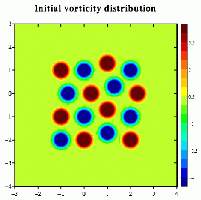
Initial vorticity distribution: 8 positive and 8 negative Bessel monopoles of radius 0.45 are placed around the centre a 7 by 7 domain, but not exactly symmetric. (You can click on the pictures for a larger version.)

In this simulation 16 single signed monopolar vortices, so-called Bessel monopoles, interact with each other in a square domain with stress-free walls all around. Initially they are placed not exactly symmetric to make things more interesting.

Initial vorticity distribution: 8 positive and 8 negative Bessel monopoles
of radius 0.45 are placed around the centre a 7 by 7 domain, but not exactly
symmetric.
(You can click on the pictures for a larger version.)
The boundary condition of stress-free walls implies that fluid cannot go through the walls, but can move freely along them. In physical terms: the velocity of the fluid perpendicular to the wall is zero, whereas the velocity tangential to the wall is undetermined. A vortex reaching such a boundary sort of 'feels' its reflection in the wall and interacts with it. The motion of each monopole is therefore determined by the 15 other monopoles and by the 'reflections' of all monopoles in the walls.
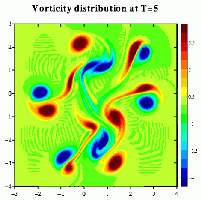
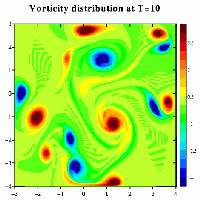
Vorticity distribution at t=5 (left) and t=10 (right).
Apparently some monopoles join with oppositely signed monopoles and form dipolar structures, while other monopoles are torn apart and merge with monopoles of the same sign to form larger monopoles. Small scale features gradually disappear and there is a tendency for the vorticity to go to larger scales. This proces is called self-organisation of two-dimensional flows. Since the initial state is not symmetrical, the evolution is somewhat chaotic.
During the evolution viscosity spreads the vorticity over a larger area and reduces the extrema of vorticity, as a result of which the monopoles move and rotate slower. The colours in the pictures stand for the same vorticity levels throughout the evoltuion shown in the pictures. The reduction of the vorticity extrema is therefore visible as a disappearing of colours as time goes on.
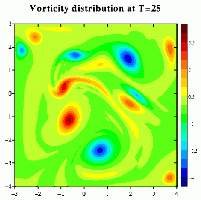
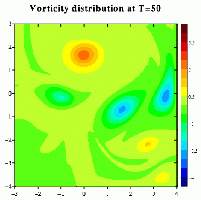
Vorticity distribution at t=25 (left) and t=50 (right).
The evolution of the vorticity distribution is computed with a Finite Difference Method which solves the two-dimensional vorticity (Navier-Stokes) equation. Time and distances are given in dimensionless units.
===> Some details on the computation presented on this page for those who are interested.
<=== Numerical simulations of 2D vortex evolution with a Finite Difference Method.
 Jos van Geffen --
Home |
Site Map |
Contact Me
Jos van Geffen --
Home |
Site Map |
Contact Me